Tetris AI – The (Near) Perfect Bot

Yiyuan Lee / April 14, 2013

In this project, we develop an AI (online demo here) which can indefinitely clear lines in a single Tetris game (I had to stop it because my lappy was burning out due to poor ventilation at some point in time).

AI after a long (2 weeks) time

Definition of game

Perhaps the most interesting observation I made in the course of developing the AI was this: despite the existence of the “standard” Tetris guideline, there are still many variants of the game. If you were to play a game of Tetris online, chances are that it won’t be the “standard” one.

For this AI, I’ve stuck to the “official” guideline as closely as possible. For the sake of reducing ambiguity, here are the rules I’ve adhered to:

The Tetris grid is 10 cells wide and 22 cells tall, with the top 2 rows hidden.
All Tetrominoes (Tetris pieces) will start in the middle of the top 2 rows.
There are 7 Tetrominoes : “I”, “O”, “J”, “L”, “S”, “Z”, “T”.
The Super Rotation System is used for all rotations.
The “7 system” random generator is used to randomize the next pieces.
One lookahead piece is allowed (the player knows what the next piece will be).

Below shows a table of all possible pieces under these rules.

Possible pieces and rotations

The best possible move

Our goal is to clear as many lines as possible, and therefore, to make as many moves as possible.

To meet this goal, our AI will decide the best move for a given Tetris piece by trying out all the possible moves (rotation and position). It computes a score for each possible move (together with the lookahead piece), and selects the one with the best score as its next move.

The score for each move is computed by assessing the grid the move would result in. This assessment is based on four heuristics: aggregate height, complete lines, holes, and bumpiness, each of which the AI will try to either minimize or maximize.

Aggregate Height

This heuristic tells us how “high” a grid is. To compute the aggregate height, we take the sum of the height of each column (the distance from the highest tile in each column to the bottom of the grid).

Aggregate Height = 48

We’ll want to minimize this value, because a lower aggregate height means that we can drop more pieces into the grid before hitting the top of the grid.

Complete Lines

This is probably the most intuitive heuristic among the four. It is simply the the number of complete lines in a grid.

Complete lines = 2

We’ll want to maximize the number of complete lines, because clearing lines is the goal of the AI, and clearing lines will give us more space for more pieces.

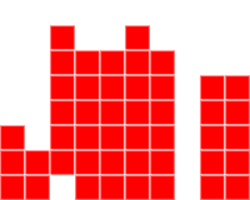
Holes

A hole is defined as an empty space such that there is at least one tile in the same column above it.

Number of holes = 2

A hole is harder to clear, because we’ll have to clear all the lines above it before we can reach the hole and fill it up. So we’ll have to minimize these holes.

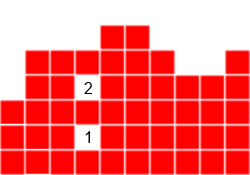
Bumpiness

Consider a case where we get a deep “well” in our grid that makes it undesirable:

An unideal grid

The presence of these wells indicate that lines that can be cleared easily are not cleared. If a well were to be covered, all the rows which the well spans will be hard to clear. To generalize the idea of a “well”, we define a heuristic which I shall name “bumpiness”.

The bumpiness of a grid tells us the variation of its column heights. It is computed by summing up the absolute differences between all two adjacent columns.

Bumpiness = 6

In the above example,

$bumpiness = 6 = |3 - 5| + |5 - 5| + ... + |4 - 4| + |4 - 5|$

To ensure that the top of the grid is as monotone as possible, the AI will try to minimize this value.

Putting the heuristic together

We now compute the score of a grid by taking a linear combination of our four heuristics. It is given by the following score function:

$a \times (Aggregate Height) + b \times (Complete Lines) + c \times (Holes) + d \times (Bumpiness)$

where $a, b, c, d$ are constant paramters.

We want to minimize aggregate height, holes and bumpiness, so we can expect $a, c, d$ to be negative. Similarly, we want to maximize the number of complete lines, so we can expect $B$ to be positive.

I used a Genetic Algorithm (GA) (explained in full detail below) to produce the following optimal set of parameters:

$a = -0.510066$
$b = 0.760666$
$c = -0.35663$
$d = -0.184483$

By using this set of parameters and the score formula, the AI can pick the best possible move by exhausting all possible moves (including the lookahead piece) and select the one with the highest score.

The Genetic Algorithm

Parameter sets, 4D vectors and the unit 3-sphere

Each possible set of parameters ( $A, B, C, D$ ) can be represented as a vector in $\mathbb R^4$ ,

$\vec{p} = \left(\begin{array}{cc}a\\b\\c\\d\end{array}\right)$

A standard Genetic Algorithm for real-valued genes would involve searching the entire solution space ( $\mathbb R^4$ ) for an optimal set of parameters. In this project, however, we need only consider points on the unit 3-sphere (i.e. 4-dimensional unit sphere). This is because the score function defined above is a linear functional and the comparison outcomes are invariant under scaling (of the score function).

To understand this from a more mathematical point of view, first rewrite the score function in the context of vectors as

$f(\vec{x}) = \vec{p}\cdot\vec{x}$

where

$\vec{p} = \left(\begin{array}{cc}a\\b\\c\\d\end{array}\right),\vec{x} = \left(\begin{array}{cc}\text{Aggregate Height} \\ \text{Complete Lines} \\ \text{Holes} \\ \text{Bumpiness}\end{array}\right)$

Suppose we want to compare between two moves, move 1 and move 2, to decide which move is “better” (i.e. gives a better score). Suppose also that move 1 and 2 produces values $\vec{x_1}$ and $\vec{x_2}$ respectively. To check if move 1 is better than move 2, we need to check if $f(\vec{x_1}) > f(\vec{x_2}) \iff f(\vec{x_1}) - f(\vec{x_2}) > 0$ . If this condition fails then it is trivial to conclude that move 2 is better or equally good as compared to move 1.

Now,

$f(\vec{x_1}) - f(\vec{x_2}) = \vec{p}\cdot\vec{x_1} - \vec{p}\cdot\vec{x_2} = \vec{p}\cdot\left(\vec{x_1} - \vec{x_2}\right)$

Suppose $\vec{p}\cdot\left(\vec{x_1} - \vec{x_2}\right)$ is either positive or negative. The better move would then be move 1 and move 2 respectively. Here, we can see how the comparison outcome is invariant under scaling of the parameters – we can multiply $\vec{p}$ by any positive real (scalar) constant and the sign of the above difference will remain the same (although the magnitude differs – but that is irrelevant), in which case the decision does not differ!

All parameter vectors in the same direction produce equivalent results. As such, it is sufficient to only consider a single vector for each direction. This justifies the restriction of the search to only points on the surface of the unit 3-sphere, as the surface of the sphere covers all directions possible.

We’ll now move on to define the fitness function, selection procedure, crossover operator, mutation operator and recombination procedure used for tuning the AI.

Fitness function

The population is first initialized with 1000 unit parameter vectors.

For each parameter vector, we run the AI for 100 games, each with at most 500 Tetromino pieces (i.e. 500 at most moves). We let the fitness $fitness(\vec{p})$ of any one parameter vector $\vec{p}$ be equal to the total number of lines cleared. The worst possible fitness is $0$ , in which case the AI clears no lines for all of the games.

Tournament selection

Parent individuals are selected for reproduction using tournament selection. We select 10% (= 100) of the population at random, and the two fittest individuals in this subpool proceed on for crossover to produce a new offspring. This process is repeated until the number of new offsprings produced reaches 30% of the population size (= 300).

Weighted average crossover

For crossover, the two parent vectors $\vec{p_1}, \vec{p_2}$ are combined using a vector form of weighted averages. The unit offspring vector $\hat{\vec{p'}}$ can then be produced where

$\vec{p'} = \vec{p_1}\cdot fitness(\vec{p_1}) + \vec{p_2}\cdot fitness(\vec{p_2})$

In essence, the offspring vector lies in between the two parent vectors on the unit 3-sphere, but leans towards the fitter parent by an amount that increases with the difference between the fitness of the two parents. This reflects the favoritism of the crossover operator towards the fitter parent.

Mutation operator

Each newly produced offspring is given a small chance (5%) to mutate. If it does indeed mutate, then a random component of the offspring vector is adjusted by a random amount of up to $\pm 0.2$ . The vector is then normalized.

As we are working with unit spheres, I would have preferred rotation of the offspring vectors by a certain angle. However, unlike rotations in 3D, 4D rotations are a lot more perplexing. As such, I have opted for the aforementioned more simple mutation operator.

Delete-n-last replacement

After the number of offsprings produced reaches 30% (= 300) of the original population size, the weakest 30% individuals in the population are deleted and replaced by the newly produced offsprings, forming next generation of the population. The population size remains the same (1000). One can then repeat the entire process until the population is fit enough, after which the algorithm terminates.

Results

The AI was implemented in Javascript and tested with Google Chrome (it also works for most other browsers). You can try it out online here. The source code for the implementation can be found here. The AI was still running after around two weeks – it had cleared 2,183,277 lines by then.

AI after two weeks

Conclusion

Through the course of this project I’ve tried out some other heuristics such as the highest column height and the number of consecutive holes.

It turns out that some of them were redundant, and some of them were replaced by better heuristics (for example, the highest column height heuristic was replaced by the aggregate height), since this produces better results.

I would also like to stress that this AI was tuned for a specific set of rules (I defined them in the first few sections of this article). The results may or may not be the same for a different set of rules.

For example, using a naive random piece generator instead may result in an obscenely long sequence of “S” or “Z” tiles which will increase the difficulty of the AI. Allowing more lookaheads will also allow the AI to make more complex moves, in which case it will probably perform better (if properly tuned).

As such, when comparing between the results of different Tetris AIs, much attention should be placed on the set of rules used for a fair comparison to be made.

31 thoughts on “Tetris AI – The (Near) Perfect Bot”

DPR says:

August 21, 2013 at 10:17 AM

“It seems that the number of lines cleared can never exceed 20% of the number of Tetrominos placed.”
This is readily explainable =) Each line will take 20 blocks if the width of the board is 20. Since each Tetromino is 4 blocks, it will take exactly 5 Tetrominos to clear a line. So the theoretical limit is that 20% of the number of Tetrominos will create cleared lines. In practice, this number will be lower since there will be Tetrominos that you placed and were not cleared when you lose. (For example, if you cleared 1000 lines with 5000 blocks but then lost with the next 200 blocks.) But the longer you can survive, the closer you get to this percentage. I noticed the same thing when I was programming a Tetris AI recently, although I was using a different width to the grid so it was a different percentage.

Out of curiosity, what’s the average lines cleared for your AI on a normal sized grid? The best I have so far is an average of ~16k lines cleared out of 1000 games. But I didn’t test bumpiness and blockages as part of the scoring as you mentioned here. Also, I didn’t use a genetic algorithm; I implemented what I call slicing for lack of a better word. It’s where I test 100 different values on the first trait, keep the best, then do a test on 100 values for the second trait while keeping the first trait, etc. Doing this requires making a few insane assumptions about the traits being linearly independent, but I found the tests to be easier (at least for me) and the results to be acceptable.
Also, did you let the AI choose where the block would start in the left-right direction or did you have it start in the middle as with the original Tetris? I found this makes an unfair, significant difference in AI capabilities, so I had to disable it being able to have the piece start at any position along the top. I originally did this because I was lazy and didn’t want to simulate the movement left-right along the top as well as down. ^^

Reply
- Lee Yiyuan says:
  
  August 21, 2013 at 11:12 PM
  
  Hi DPR,
  
  That’s a very nice explanation for the 20%, perhaps we could establish some more general relationship which provides the limit for a specific width.
  I haven’t tested for normal sized grid, but I’ll update it in the future such that the size of the grid can be set. Initially I left out bumpiness as well (too many parameters is a pain when it comes to the genetic algorithm), but when I tried it, the AI seemed to perform better.
  As for the left-right advantage, nope, I didn’t make it start from the middle as well (because I was lazy too xD). But you’re right, it’s rather unfair. I’ll look into changing the AI’s behavior such that the tetris blocks come down from the center.
  
  Thanks again for the comment and keep them coming! ^^
  -Yiyuan
  
  Reply
- Lee Yiyuan says:
  
  May 25, 2014 at 5:58 PM
  
  Hello there once again DPR!
  
  I’ve since updated the rules to the one specified by the “Official” Tetris Guidelines (http://tetris.wikia.com/wiki/Tetris_Guideline). I’ve also shifted the AI online as a Javascript app – it’s hassle free! Do check out the results.
  
  Thanks!
  -Yiyuan
  
  Reply
  - DPR says:
    
    November 27, 2014 at 4:49 AM
    
    It looks very nice =) For demonstration purposes, the Javascript app works very well at making it easier for people to test. I looked through the Javascript source. It was quite interesting to see places where you’ve implemented some things similarly to me, and other places where things were done differently. There’s rarely one right way to do it, but some approaches do seem to be so good that people will naturally tend towards using them. Using a for loop to check all the different rotations’ optimum scores, for example.
Pingback: 2048 AI – The Intelligent Bot | Code My Road
Tony says:

March 7, 2015 at 11:35 AM

This is really good. I would usually turn off the ai and mess him up a little and turn him back on to see how well he could fix it up. Did pretty well can’t get to crazy but yeah. Now what i’m saying is instead of having it speed it up by pushing the down button is for it to push space instead for it to be able to place the block very fast.

Reply
bengoldberg says:

April 2, 2016 at 12:01 PM

What if piece selection was not random, but instead tetrominoes were chosen chosen by another AI, one whose “goal” is to make the player lose?

Reply
- Lee Yiyuan says:
  
  April 2, 2016 at 5:07 PM
  
  That is a good question. In that case, we can redesign the AI to consider the game as a two-player game and to use Minimax instead to compute the score of each decision for each move.
  
  It will be quite similar to looking ahead, except that the AI now assumes that the next few pieces are pieces that will minimize its future overall scores.
  
  Reply
  - Umar Khan says:
    
    July 27, 2016 at 12:22 AM
    
    I believe in standard Tetris a long enough sequence of S, Z pieces inevitably leads to a loss so the second AI will always win when that limit is reached.
Mitch says:

April 12, 2016 at 11:34 PM

What a nice piece of work 🙂
But yet there is one thing that leaves me a bit confused: Shouldn’t there be a difference between the rating of a grid with a big hole and a grid with a small hole?
Like this:

XXXX
XXXX
XX_X
XXXX

and this:

XXXX
XX_X
XX_X
XXXX

(Where X is a tile and _ is a hole)

It seems that those two grids get the same grid score. Should’t be the second grid less desirable?

Thanks,
Mitch

Reply
- Lee Yiyuan says:
  
  April 13, 2016 at 12:00 AM
  
  Yes indeed. Any empty space with at least one tile above it in the same column is defined to be a “hole”. It may be less intuitive and more axiomatic indeed to infer from this definition that in the second case you have stated, two “hole”s exist instead of just one 🙂
  
  Reply
  - Mitch says:
    
    April 13, 2016 at 6:59 PM
    
    I see.
    Yet, there is another question i am clueless with, maybe you have an opinion on this:
    
    You wrote: “The score for each move is computed by assessing the grid the move would result in”.
    
    I think a move not finished when the piece is places, but when additionally all the complete lines are cleared.
    Because (for example) holes that appear when placing the piece can disapper after a line has been cleared.
    
    You calculate the grid score without clearing complete lines. Doesn’t that distort the grid score?
  - Yiyuan Lee says:
    
    April 13, 2016 at 10:21 PM
    
    Indeed, by not clearing the lines first, this particular component appears to have quite a bit of conflict with the other three components.
    
    However, for this project, I did not clear the lines first before calculating the score because back then, I had thought that the immediately resulting grid would provide more information for the AI to work with to produce better results.
    
    Perhaps by clearing the lines first before calculating the grid score, the “number of complete lines” component may actually turn out to be redundant. It is possible to alter the AI such that it clears lines first before computing the grid score, and such that the “number of complete lines” component is no longer included in the computation of the grid score. By running tests on the altered AI it is possible to determine if it fairs at least as well as the current version.
  - Mitch says:
    
    April 13, 2016 at 11:26 PM
    
    Yeah, i think so too, clearing the lines first before calculation the grid score >might< make the "numberOfCompleteLines" component redundant, because clearing the lines makes the aggregate height become much smaller which is, of course, desirable, making the moves that result in cleared lines have a higher grid score.
    I think the most interesting question here is: does removing the "numberOfCompleteLines" result in a different bot behaviour? Maybe the best move stays the same when calculating the grid score after clearing the lines.
Chris says:

July 17, 2016 at 11:09 PM

Hi Lee,

what an awesome project! I’m currently trying to understand genetic algorithms to solve a quite similar problem. What I didn’t quite understand after reading your article is how you computed the Parameters.
In your JS code those parameters are hardcoded, so I assume you had some other code that computed them? When I change them the AI still seems to work, just not as good apparently.
I would be interested to see how to actually compute them.

Keep up the nice work 🙂

Reply
- Yiyuan Lee says:
  
  July 27, 2016 at 12:10 PM
  
  Hi Chris,
  
  Unfortunately the computation of the parameters were quite some time ago and I no longer have the code available with me.
  For the sake of completeness, I may rewrite the optimization code again sometime soon in the future after I am done with my conscription term.
  The methods used in the optimization were exactly as described in the article and you may refer to them for a general idea as of now.
  
  Cheers!
  
  Reply
  - RY says:
    
    December 8, 2017 at 1:45 PM
    
    Hey, just wanted to say: Amazing work! I was wondering if you got around to rewriting the optimization code?
  - Yiyuan Lee says:
    
    December 8, 2017 at 2:11 PM
    
    Yes, at the moment there is already a tuner that you can use to do the genetic tuning. You can check it out on the github repo 🙂
  - RY says:
    
    December 29, 2017 at 3:17 AM
    
    Ah, got it. Thanks for the reply!
Tizen Ye says:

March 21, 2017 at 1:58 PM

Hi Lee,
Really awesome project and I am a fan of Clannad too!

Reply
- Yiyuan Lee says:
  
  March 21, 2017 at 2:00 PM
  
  :>
  
  Reply
Toolz says:

September 16, 2017 at 2:31 PM

Cool. BUT Can u show me how to slow down the speed of one piece while AI is running? wanna look this AI in slow motion :))). Thanks a lot ❤

Reply
Samuel says:

November 8, 2017 at 11:56 AM

I know this project is very old but if you could consider tetrises and holds that would be excellent.
the standard playfield is 10 cells wide and at least 22 cells high, with the topmost two hidden, with this information we need to perfectly stack the pieces in a 9 by 20 playfield and this way we can use the hold option to hold the 1 by 4 pieces and send tetrises whenever we can. By creating code for this your AI will beat any human on earth. Keep up the great work!!!

a 13 year old who is very interested in tetris

Reply
Pingback: How to Make an Evolutionary Tetris AI | Online Coding
tetris-problem says:

April 29, 2018 at 8:54 PM

hello,i appreciate your great idea very much, i wonder that if you just use the heuristics formula to achieve your AI, if so，would you please tell me the number of your heuristics lookaheads you calculate for every piece, for i tried use your method to achieve tetris AI without any heuristics lookahead and its failed,Thank you very much!

Reply
tetris-problem says:

April 29, 2018 at 9:32 PM

i just read your code,my understand is that in your code the next n pieces is defined in advance rather than random?thank you!

Reply
Pingback: How to make a Tetris bot? – Nope++
Ben Does Gaming says:

May 21, 2018 at 7:26 PM

Thank you for this. Not only is it interesting, but this may help me with developing an AI for a two-player Tetris game that I am coding. I will give credit for inspiration, but I also hope to be able to use some of the theories/concepts explained within to create my own AI. Regardless, this gave me a starting point to work from, and for that I thank you.

Reply
Ren says:

June 17, 2018 at 8:29 PM

But shouldn’t height be counted without cleaned lines or what? Did I miss something?

Reply
rajiv says:

September 27, 2018 at 4:17 PM

I’m impressed.May I get all the analysis and explanation in clear with moves as example?I’d appriciated If I get through mail rajivkumarmarrapu@gmail.com

Reply
Pingback: How to make a Tetris bot? – Coconut Shibe